NVIDIA : Tensor core
Tensor core는 NVIDIA GPU volta architecture(2018)부터 등장한 Matrix multiply-accumulate (MMA) 연산을 지원하기 위한 specialized computing unit이다. 다양한 NPU(Google의 Tensor Processing Unit 등)들과 같이, 딥러닝이 대세가 되고 matrix-multiplication이 많은 애플리케이션에서 주요한 성능 병목이 되면서 NVIDIA가 GPU에도 탑재한 것으로 생각된다.
이번 포스트에서는 다음 논문을 읽고 Tensor core에 대하여 정리해보고자 한다. Programmability와 성능, 한계 등에 대하여 매우 자세히 분석해놓은 논문이다.
Markidis, Stefano & Chien, Steven & Laure, Erwin & Peng, Ivy & Vetter, Jeffrey. (2018). NVIDIA Tensor Core Programmability, Performance & Precision. 522-531. 10.1109/IPDPSW.2018.00091.
(2018년 Volta architecture를 기반으로 작성된 논문으로 Turing, Ampere 아키텍처로 발전하면서 추가된 기능(ex, integer, double presion floating point 연산 등)에 대한 내용은 없다)
Introduction - Volta architecture
Tesla V100 GPU는 다음과 같은 아키텍처를 가진다.

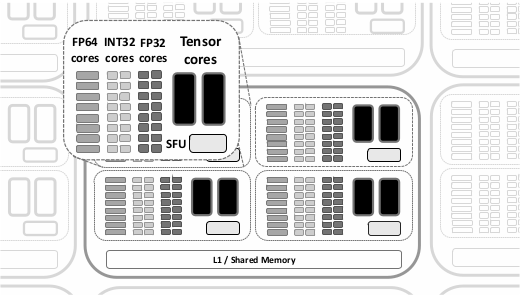
위 그림에 나오듯이 V100은 2,560(=80*4*8) FP64 cores, 5,120(=80*4*16) FP32 cores, 640(=80*4*2) Tensor cores를 가진다. Half precision floating point 연산에 대한 이론적인 성능은 FP32 cores를 사용할 경우 31.4 Tflops/s까지 나오는데 비해, Tensor cores를 사용하면 125 Tflops/s까지 나온다고 한다.
Tensor core 디테일
그렇다면 왜 기존의 cuda core에 비해 tensor core가 더 좋은 성능을 달성할 수 있을까? 앞서 말했듯이 tensor core는 4*4 matrix에 대한 MMA (논문에서는 Fused multiply add, FMA라고도 씀) operation을 1 GPU clock cycle에 처리될 수 있도록 회로가 구현된다. 즉 하나의 tensor core는 64번의 MMA 연산을 수행할 수 있으며, 640개의 tensor cores가 있기에 one clock cycle 당 총 40960번의 MMA 연산, 즉 81920번(곱셈+덧셈)의 floating-point 연산을 수행한다고 한다.

다만 tensor core는 Volta 아키텍처 출시 당시, FP16 연산만을 지원했다고 한다. 현재는 Integer와 TF32-19bit operand 연산도 지원한다. 그렇지만 16bit operand가 입력으로 들어올때 tensor core는 최대의 성능을 발휘한다.
요즘 AI 경량화 등 AI 애플리케이션에서 FP32 parameters가 아닌 FP16 parameters를 쓰는 연구가 많이 진행되고 있고, 예측 정확도는 유지하면서 학습 및 추론 시간을 단축시킨 결과가 많이 보고되고 있다. 따라서 tensor core가 AI 애플리케이션에 충분히 잘 이용될 수 있을 것이다.
다른 HPC 애플리케이션에서의 활용
그렇다면 AI 애플리케이션이 아닌 다른 High Performance Computing (HPC) 애플리케이션에서도 tensor core가 충분히 잘 이용될 수 있을까? 16bit 연산만으로는 충분하지 않을 것이라 생각한다.

위 그림은 IEEE 754 FP16의 format이다. Exponent가 5bit, faction이 10bit 밖에 되지 않으니 논문에서는 다음과 같은 문제가 발생한다고 한다.
- Limited range: -65,504~+65,504까지 표현 가능 (expoent가 5bit이니 2의 15승 * fraction은 1.11...까지 표현되니 65504까지 인것 같다.)
- Decreasing precision with increasing value range intervals: fraction이 10bit이니 같은 exponent를 가지는 숫자들은 총 2의 10승=1024개밖에 존재하지 않는다. 즉 2의 15승~2의 16승 사이 숫자 중 1024개만을 표현할 수 있다.
계산의 정확도가 요구되는 계산과학 문제에서는 FP16이 사용되기 어려워 보인다. 그래서 이 논문은 FP16연산으로 FP32연산을 할 수 있도록 precision refinement 알고리즘을 소개한다.
Ra = Asingle - Ahalf, 즉 16진수 변환 과정에서 사라지는 residual 값(마찬가지로 FP16)으로 정의한다. 그렇다면 다음 식과 같이 FP16 연산으로 표현할 수 있다.

위 방식은 precision을 보완할 수 있지만, range만은 보완하지 못한다. 그렇지만 4번의 FP16 MMA 연산을 통해 1번의 FP32 연산을 어느정도 정확도로 구현할 수 있다.
Tensor core 이용 예
다음 프로젝트는 cublas에서 제공하는 tensor core gemm API를 사용한 예시이다. cuda core를 사용한 gemm 성능과 tensor core를 사용한 gemm 성능을 비교할 수 있을 것이다. (readme 파일도 없고, 주석도 없는 장난 수준의 프로젝트이다. 빠른 시일 내로 설명을 추가할 예정이다.)
https://github.com/jhson989/tensor_core_test
GitHub - jhson989/tensor_core_test
Contribute to jhson989/tensor_core_test development by creating an account on GitHub.
github.com