| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- SpMM
- dnn
- 양자역학의공준
- 반도체기초
- POD
- jhVM
- Semiconductor
- cloud
- CUDA
- quantum_computing
- Compression
- 딥러닝
- kubernetes
- 클라우드
- 쿠버네티스
- CuDNN
- Qubit
- C++
- HA
- stl
- deep_learning
- DRAM
- 반도체
- GPU
- convolution
- jhDNN
- flash_memory
- nvidia
- FPGA
- sycl
- Today
- Total
Computing
SpMM - 2 : Sparse Matrix Representation 본문
SpMM - 2 : Sparse Matrix Representation
jhson989 2022. 3. 22. 21:24이전 포스터에서 sparse matrix가 무엇인지를 정의하고 왜 필요한지를 알아보았다.
SpMM - 1 : Introduction
Sparse Matrix Multiplication Matrix multiplication은 우리가 흔히 아는 다음 그림과 같은 행렬곱을 의미한다. Matrix multiplication(MM) 연산은 기존의 선형대수 관련 문제 계산, 3D graphics 뿐만 아니라..
computing-jhson.tistory.com
Matrix Representation in Memory
메모리에 행렬을 저장할 시, 행렬을 2차원 array로 저장하면 array의 인덱스가 각 행렬성분의 위치, array의 값이 각 행렬성분의 값을 나타낼 수 있어서 편리하다.
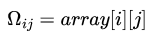
이때 sparsity가 0.01인 100*100 sparse matrix에서 0이 아닌 성분의 개수는 100개이며, 나머지 9900개는 0이다. 메모리에 저장할 시, 모든 요소를 다 저장하는 대신 0이 아닌 성분만을 저장하면 많은 메모리 사용량을 아낄 수 있을 것이다.

이를 위해 array 형태가 아닌 다양한 방식의 행렬 저장 형식이 제안되고 있다. 각각의 방식 중 어떤 방식이 좋다는 것은 없고, 각 포맷으로 저장된 희소행렬을 사용하는 애플리케이션(알고리즘)에 따라 혹은 각 희소행렬의 특징(ex, structed or unstructed)에 따라 가장 효율적인 저장방식이 결정된다고 한다.
이번 포스팅에서는 대표적인 COO (coordinate format), CSR (Compressed sparse row format), ELL (ELLPACK/ITPACK format)에 대하여 소개하고자 한다.
COO Representation
COO 방식은 행렬 중 0이 아닌 요소의 위치 (row, column 좌표)와 값만을 저장하는 가장 단순한 방식이다. 3가지 값(행렬의 row 좌표, column 좌표, 요소의 값)을 row array, col array, val array에 저장하며, 다음 식을 만족한다.

(row, col) 쌍에 저장되지 않은 행렬의 좌표는 0이라고 생각한다.
희소행렬 Ω을 그림과 같이 정의하면,

희소행렬 Ω의 row, col, val array는 다음과 같다.

희소행렬 Ω의 (0,4) 요소인 9를 표현하기 위해, row[0], col[0], val[0]에 각각 0, 4, 9를 저장하였으며, 희소행렬 Ω의 (6,1) 요소인 7를 표현하기 위해, row[6], col[6], val[6]에 각각 6, 1, 7를 저장하였다.
CSR Representation
CSR 방식은 COO 방식을 조금 더 압축한 것이다.

row array를 없앤 대신 rowptr array를 사용한다. rowptr[i]=j는 col array의 j번째 인덱스부터 i번째 row와 매칭이 된다는 것을 나타낸다. 예를 들어 위 그림에서 rowptr[6] = 6, rowptr[7] = 9인데, 이는 col[6], col[7], col[8]의 row는 6이고, col[9]의 row는 7이라는 것이다. 따라서 다음과 같음을 알 수 있다.

rowptr[5] = 4이고, rowptr[6] = 4이다. 이 말은 col[4]이상 col[4]미만 row 5와 매칭된다는 것으로 row 5와 매칭되는 col은 없다는 것이다. 행렬 Ω의 5번째 row의 모든 요소는 0임을 확인할 수 있다.
CSR 방식은 rowptr array의 크기가 0이 아닌 성분의 개수에 독립적으로 행렬의 row 개수와 같다는 장점이 있다.
ELL Representation
ELL 방식은 좀 더 알고리즘과 연관된 표현방법이다. 밑의 그림과 같이 col, val array만으로 표현할 수 있으며 COO 방식가 비슷하게 col, val을 구성하지만, 추가적으로 col에 0을 padding 하였다. 행렬 Ω의 0이 아닌 요소를 가장 많이 가진 row의 0이 아닌 요소의 개수 (여기서는 6번째 row, 총 3개)에 맞게 모든 row를 padding시킨다. 따라서 col array의 3개 요소씩 하나의 row에 매칭(0~2=row-0, 3~5=row-1, ...)되며, col[i]는 (i/3)-번째 row와 매칭된다.

이와 같은 방식은, multiple threads가 한 row씩을 맡아 계산을 처리하는 알고리즘에서 thread들마다 balanced work를 가질 수 있어서 좋다. 위의 예시에서는 모든 row는 3가지 요소를 가지므로 (pad된 값 포함), 모든 thread는 3가지 요소 처리를 맡아서 한다. SIMD 머신에서는 branch divergence가 최대한 없는 게 좋기에, 이 표현법은 각 threads의 일의 개수가 통일되기에 좋다고 한다.
다만 한 메모리 사용이 증가할 수 있으며, 특히 하나의 row에 0이 아닌 요소가 집중될 경우 메모리 사용량이 급격히 커질 수 있다. 이를 위해 Sliced-ELL 등의 방식이 제안된다.
'Parallel | Distributed Computing > 알고리즘' 카테고리의 다른 글
| BLAS란? (AXPY, GEMV, GEMM 연산자) (0) | 2022.07.07 |
|---|---|
| Parallel Matrix Transpose : Coalesced Memory Access & Bank Conflicts (SYCL 구현) (0) | 2022.04.27 |
| SpMM - 3 : CSR 변환 GPU 병렬 알고리즘 (0) | 2022.03.29 |
| SpMM - 1 : Introduction (0) | 2022.03.22 |
| Algorithm) Parallel Merge sort (0) | 2022.03.10 |




