| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- 클라우드
- HA
- SpMM
- quantum_computing
- GPU
- cloud
- DRAM
- 반도체
- jhDNN
- Semiconductor
- 양자역학의공준
- CUDA
- Compression
- dnn
- POD
- 쿠버네티스
- 딥러닝
- sycl
- CuDNN
- nvidia
- flash_memory
- stl
- FPGA
- jhVM
- kubernetes
- 반도체기초
- convolution
- deep_learning
- C++
- Qubit
- Today
- Total
Computing
Semantic Segmentation (2) : U-Net architecture, Transposed Convolution 연산 분석 본문
Semantic Segmentation (2) : U-Net architecture, Transposed Convolution 연산 분석
jhson989 2022. 6. 2. 20:59이전글
이전글에서 Semantic segmentation란 무엇인지에 대하여 정리하였다. 또한 Semantic segmentation 문제를 풀기 위한 딥러닝 네트워크(SSN)의 도전 과제 및 FCN 네트워크에 대해서도 정리하였다. SSN은 어떤 물체가 있는 지(classification), 어디에 있는 지 (localization)을 one-shot으로 추론하도록 학습된다.
Image feature extraction에 강한 convolution 기반의 딥러닝 네트워크(CNN)들은 image classification 영역에서 좋은 성적을 보여왔다. 따라서 SSN 분야의 도전 과제는 어떻게 하면 classification의 성능을 유지하는 동시에, 그 과정에서 사라지는 (압축되는) 지역 정보(localization)를 더 잘 보존할 것인지가 될 것이다. 이를 위해 FCN은 fully connected layter 제거, skip connection을 통한 압축이 덜 된 정보 보존 & 전달, transposed convolution layer를 활용한 upsampling 학습, 3가지를 제안하였다.
오늘은 FCN에서 발전하여, skip connection 및 localization 과정을 강화한 U-Net[1]에 대하여 정리하고자 한다.
U-Net Architecture

논문 [1]이 제안한 딥러닝 네트워크를 U-Net이라고 부르는데, 알파벳 U를 닮아서 지어진 이름이다. U-Net은 이미지의 특징 추출을 위한 contracting path (이미지의 왼쪽), 정확한 localization을 위한 expanding path (이미지의 오른쪽)로 구성된다.
Contracting path는 object classification에 강한 전통적인 CNN 구조를 가진다. Convolution layer를 통해 이미지의 local 패턴을 추출하고, max pooling layer를 통해 이미지의 특징을 추상화(압축)해 global 패턴을 추출한다. 이 과정을 통해 이미지의 global 특징을 추출한다. 다만 이미지가 추상화(압축)되면서 개별 pixel의 정보는 사라진다.
Convoluion layer 자체가 spatially 이웃한 픽셀들끼리의 관계를 도출하기에 어느 정도 위치 정보는 기억이 된다. 즉 Fig 1.에서 가장 많이 추상화된 512*32*32 feature map에서도 위치 정보가 보존되어 있다는 것이다. 만약 이미지의 오른쪽에 개가 있다면, 압축된 512*32*32 feature map의 오른쪽에도 개를 의미하는 정보가 어느정도 포함되어 있을 것이다. (이게 FCN이 작동할 수 있는 가장 근본이 되는 아이디어일 거라고 생각한다.) 다만 문제가 되는 것은 개별 pixel 하나 하나의 정보는 사라진다는 것이다. FCN에서는 skip connection을 통해 이를 어느정도 보완하였다.
U-Net은 이를 해결하기 위해 expanding path를 강화하는 방향을 택하였다. 즉 expanding path를 contracting path만큼의 중요성을 두고 설계하였고, 그에 따라 모양도 U자가 되었다. 또한 추상화된 feature map을 확대(up-sampling)하는 과정에 매번 skip connection을 두어, 위치 정보가 보존된 feature map을 추론 과정에서 고려할 수 있게 하였다.
다만 입력 인풋은 572*572 사이즈의 이미지이고, 출력은 392*392 사이즈의 segmentation map이다. 이는 up-sampling 과정에서 padding을 두지 않고 convolution 연산을 했기 때문으로, U-Net의 overlap-tile 전략을 위해서 이렇게 설계된 것이지 않나 생각한다. U-Net은 본래 메디컬 이미지 분석을 위해 설계된 네트워크로, overlap-tile 전략 및 메디컬 이미지의 사이즈를 고려하여 네트워크를 설계한 것 같다. 따라서 목적에 따라서 네트워크 사이즈를 조절하면 될 듯하다.
U-Net의 구조는 contracting path와 expanding path를 같은 비중으로 두고 네트워크를 설계한 것으로, encoder - decoder 구조와 비슷한 모습을 보인다. 다만 encoder에서 삭제되는 정보를 decoder가 고려할 수 있도록 skip connection을 연결해주었다. 따라서 개인적인 생각으로는 내부적으로 attention 메커니즘이 들어가지 않았나 생각한다. Decoder(expanding path)가 encoder(contracting path)가 추출한 global feature뿐만 아니라, 각 pixel의 위치 정보까지 직접 보고 판단할 수 있는 길이 있기 때문이다.
Transposed Convolution Operation
(개인적으로는 가장 직관적인 구현이 어려운 연산이다.) Transposed convolution 연산은 up-sampling 과정에서 사용되는 학습가능한 딥러닝 연산자이다. Convolution 연산의 한 때는 역연산(de-convolution)이라는 이름으로도 불렸지만, 딥러닝에서는 그러한 용도로 사용되지도 않기에 transposed convolution이라고 부르는 것이 맞다고 생각한다.
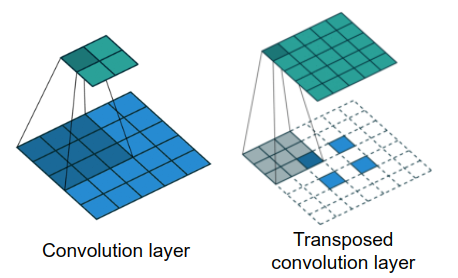
Fig 2.는 convolution 연산과 transposed convolution 연산을 잘 비교하여 나타낸 그림이다. Convolution 연산은 지역적인 (3*3) feature들끼리의 correlation(convolution)을 계산하는 연산으로 convolution 결과 feature map의 크기는 일반적으로 작아지거나 크기를 유지한다. Transposed convolution는 feature map의 크기를 키우는 up-sampling 과정에서 많이 사용되는 연산으로, 소수의 feature들로부터 더 많은 개수의 feature들을 추론하는 목적으로 사용된다.

Fig 3. 은 convolution 연산을 matrix multiplication 연산으로 변환하여 계산하는 기법을 나타낸 그림이다. 관련 설명은 이전 글에서 확인할 수 있다. 왼쪽은 convolution 연산을, 오른쪽은 transposed convolution 연산을 나타낸 것이다.
왼쪽의 경우, 3*3 kernel을 통해 4*4 input feature map에서 2*2 output feature map을 구하는 예제이다. 오른쪽의 경우, 3*3 kernel을 통해 2*2 input feature map에서 4*4 output feature map을 구하는 예제이다. 이처럼 transposed convolution은 일반 convolution의 인풋과 아웃풋 크기를 바꾼 연산이다. 또한 filter의 경우 convolution 연산의 filter matrix를 transpose한 shape를 transposed convolution 연산은 filter matrix의 shape로 가진다.
Transposed convolution 연산의 아웃풋 크기는 같은 stride, padding값을 가지는 convolution 연산의 인풋 크기와 같다. 마찬가지로 transposed convolution 연산의 인풋 크기는 같은 stride, padding값을 가지는 convolution 연산의 아웃풋 크기와 같다. 이를 통해 transposed convolution 연산의 아웃풋의 크기를 알 수 있다. I를 input size, S를 stride, K를 kernel 사이즈, P를 padding 사이즈, O를 output size라 하면, O는 Eq 1. 과 같이 구할 수 있다.

딥러닝에서 tranposed convolution이 많이 쓰이는 또 다른 이유는 convolution 연산의 back-propagation을 계산할 때 사용되기 때문이다. 3*3 convolution 연산에서 9개의 feature를 이용해 1개의 feature를 계산하는데, 3*3 transposed convolution 연산에서는 1개의 feature를 이용해 9개의 feature를 계산한다. 두 관계는 역(?, 실제 값을 역연산 하는 건 아니고, 그 관계 convolution에서 feature 1개를 만들기 위해 사용되는 feature 9개랑, transposed convolution에서 feature 9개를 만들기 위해 사용되는 feature 1개의 연관관계가 같다.)이기에 convolution 연산의 back-propagation은 transposed convolution과 동일한 연산이다.
Reference
[1] Ronneberger, O., P. Fischer, and T. Brox, 2015. U-Net: Convolutional Networks for Biomedical Image Segmentation, In: Navab N., Hornegger J., Wells W., Frangi A. (eds), Proc. of Medical Image Computing and Computer-Assisted Intervention – MICCAI 2015, Munich, DE, Oct. 5-9, vol. 9351, pp. 234-241
[2] https://zzsza.github.io/data/2018/02/23/introduction-convolution/
[3] Nrupatunga



