Compression - 4 : Quantization (2) Post Training Quantization 분석 (Calibration, TensorRT)

이전글

2022.03.29 - [Deep Learning/Optimization (Algorithm)] - Compression - 1 : Overview

2022.04.29 - [Deep Learning/Optimization (Algorithm)] - Compression - 2 : PyTorch Pruning Tutorial 및 계산 속도가 빨라지지 않는 이유

2022.06.15 - [Deep Learning/Optimization (Algorithm)] - Compression - 3 : Quantization 개념 (1)

 

지금까지 딥러닝 네트워크의 효율적인 배포를 위한 네트워크 압축(compression) 기술들 및 그 중 quantization 기법에 대하여 정리하였다. 오늘 포스터에서는 quantization 기법 중 하나인 "Post Training Quantization"(PTQ)에 대하여 정리하고자 한다. 실제 딥러닝 제품 배포환경에서 사용되는 TensorRT quantization[1][2]의 PTQ 방식을 기반으로 하여 정리하였다.

 

 

 

Post Training Quantization 목표

Quantization은 이미 학습이 완료된 네트워크에 대하여 FP32 연산을 INT8 연산으로 변환하여 추론(Inference) 속도 향상 및 메모리 최적화를 달성하고자 한다. 이전 포스터에서 보았듯, FP32 데이터를 INT8로 변환하여 계산하고 다시 FP32로 변환하는 과정에서 정보의 손실이 발생할 수 있다. 이는 네트워크 정확도 하락이라는 부작용을 초래할 수 있다. 따라서 네트워크 정확도 하락을 최대한 방지하는 FP32 -> INT8 변환법을 찾는 것이 quantization의 목표이다.

 

Fig 1. Quantization을 위한 가장 기본 변환법 [2]

 

Fig 1.은 quantization (FP32 -> INT8 변환)을 위한 가장 기본 변환법을 보여준다. 자세한 설명은 이전 포스터에서 확인할 수 있다. 해당 변환은 Symmetric linear(uniform) quantization이라고도 하는데, Eq 1.과 같이 0을 중심으로 하여 FP32 값을 linearly INT8 영역으로 맵핑하는 것을 의미한다. 이때 max값을 threshold를 통해 제한하여, 정보 손실을 줄인다.

 

Eq 1. Symmetric uniform quantization, F는 FP32 array, Q는 INT8 array

 

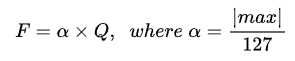
어떤 max or threshold or α를 선택하는 지에 따라서 정보 손실 정도가 달라진다. Post Training Quantization(PTQ)은 이미 학습이 완료된 네트워크를 통계적으로 분석하여, 가장 정보 손실 정도가 작은 max or threshold or α 를 선택하는 것을 목표로 한다.

 

간단하게 설명하면 다음과 같다. 기존 FP32 딥러닝 네트워크의 모든 quantizable layer에 대하여 출력값의 분포를 분석한다. 이후 다양한 threshold 값에 대하여 layer를 INT8 타입으로 변환한 후, INT8 layer의 출력값의 분포를 기존 FP32 layer의 출력값과 비교한다. 최종적으로 두 출력값의 분포의 차이(*)가 가장 적은 threshold 값을 선택하여 α를 결정한다. 이러한 최적의 α를 찾고, 이를 통해 FP32 layer를 INT8 layer로 변환하는 전 과정을 calibration이라고 한다.

 

 

 

정보의 손실 측정 : Kullback-Leibler Divergence

앞서, calibration은 기존 FP32 타입 layer의 출력값 분포와 변환된 INT8 타입 layer의 출력값 분포의 차이가 가장 작아지는 α를 찾는 것을 목표로 한다고 하였다. 이때 두 분포의 차이는 Kullback-Leibler divergence를 통해 측정한다.

 

Kullback-Leibler divergence는 relative entropy 혹은 information divergence라고도 하는데, 두 확률분포의 차이를 측정하는 함수[3]이다. 특히 어떤 확률분포에 대하여 그것을 근사하는 다른 확률분포를 생성할 때, 어느 정도 손실이 발생하는 지를 측정하는 데에 주로 사용한다. 아마 대부분 딥러닝의 loss function에 대하여 학습하면서 많이 배웠을 것이다. Fig 2.에서 보듯, 두 확률 분포 p, q에 대하여 두 확률분포가 가지고 있는 정보가 얼마나 차이가 나는지를 구할 수 있다.

 

Fig 2. Kullback-Leibler divergence의 시각적 이해 [3]

 

Quantization에서는 FP32 layer 출력값의 분포인 이산확률분포 P와 INT8 layer 출력값의 분포인 또다른 이산확률분포 Q와의 차이를 측정, 어느정도 정보의 손실이 발생하는 지를 파악하는데 KL divergence를 사용한다. 

 

Eq 2. KL-divergence 측정 공식

 

Eq 2.는 이산확률분포 P, Q에 대하여 KL divergence를 측정하는 공식이다. Calibration 과정은 FP32 layer 출력값의 분포인 P에 대하여 가장 작은 KL divergence 값을 가지는 INT8 layer 출력값의 분포 Q와, 그때의 α를 찾는 것이다.

 

Fig 3. 다양한 네트워크 layer의 출력값 분포. [2]

 

Fig 3.은 FP32 layer의 출력값 분포의 예시를 나타낸 것이다. 가로축은 출력값의 크기, 새로축은 출력값의 개수(비율)을 나타낸 것으로, N개의 출력값이 있을 때 그 출력값들의 크기 분포를 histogram화한다. (히스토그램에서 모든 출력값이 0 이상인 것을 알 수 있는데, ReLU 이후 측정되었기에 그런 것이 아닐까 추측한다.)

 

 

 

Post Training Quantization 설명

Calibration 과정을 요약하자면 다음과 같다.

 

• 딥러닝 네트워크의 모든 layer들에 대하여
  • Calibration dataset을 이용하여 FP32 layer의 출력 분포 계산
  • 다양한 threshold를 이용하여 calibration 진행 -> INT8 layer 생성
  • Calibration Dataset을 이용하여 INT8 layer의 출력 분포 계산
  • 가장 KL divergence가 작은 threshold 선택
  • 최적의 α 계산 및 INT8 데이터타입으로 layer 변환

 

Calibration dataset은 calibration 시 layer의 출력 분포를 계산하기 위해서 사용되는 데이터셋이다. 이 데이터셋을 통해 INT8 layer의 정확도가 측정되기에, 이상적으로는 실제 사용되는 데이터셋의 특징을 모두 담고 있어야 좋다. 당연히 데이터셋 속 데이터가 다양하고 개수가 많으면 좋지만 데이터셋의 크기가 증가하면 calibration 과정에 소요되는 시간이 늘어난다. 따라서 적절한 데이터셋을 선택하는 것이 중요한데 데이터셋을 선택하는 것은 프로그래머의 몫이다.

 

Fig 4. Calibration 이후 layer 출력값의 분포 변화 [2]

 

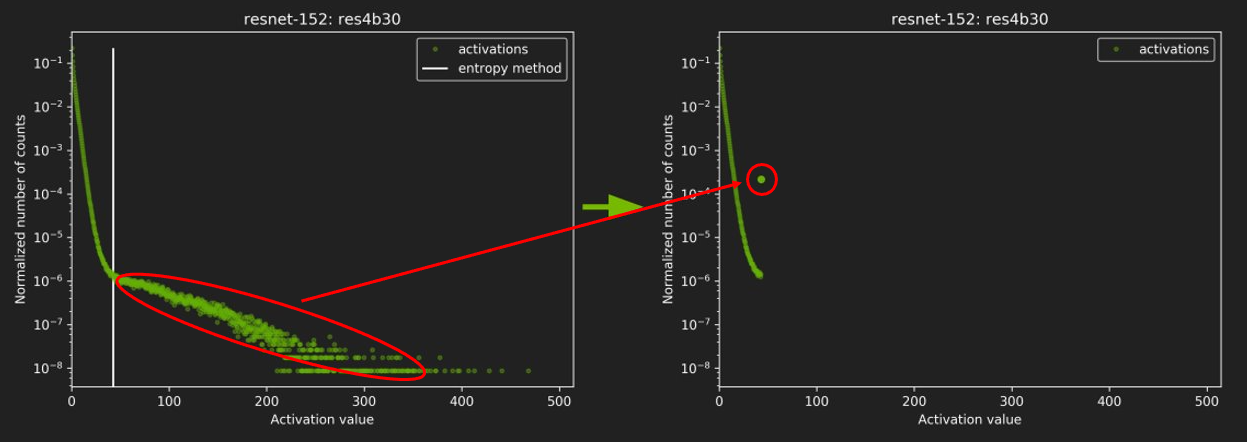
Fig 4.는 calibration 과정 이후, resnet-152의 res4b30 layer의 출력값 분포의 변화를 보여준다. 왼쪽은 기존 FP32 layer의 출력값의 분포이며, 오른쪽은 양자화된 INT8 layer의 출력값의 분포이다. 왼쪽 분포에서 흰색 선이 threshold를 나타내며, calibration 결과(오른쪽 분포) threshold 이상의 값을 가지는 출력값들은 모든 threshold 값으로 saturation되었다. 그림에서는 이 출력값의 개수가 많아보이지만, 세로축이 log scale이기에 실제로는 전체 출력값 중 약 0.01 퍼센트(세로축을 보면 약 10의 -4승)만을 차지한다.

 

Fig 4.에서 볼 수 있듯이, 양자화 이후에는 딥러닝 네트워크의 출력값이 어느 정도 변한다. 이게 어느정도 심각한 영향을 끼치는 지는 (아직까지는) 계산될 수 없을 것 같은데, 정확도가 크게 떨어지지 않는 모양이다. Fig 5.는 TensorRT calibration을 통해 양자화된 네트워크들의 정확도를 보여주는 표이다.

 

Fig 5. ILSVRC2012 validation dataset에 대한 기존 네트워크와 TensorRT를 통해 양자화된 네트워크의 정확도 비교 [2]

 

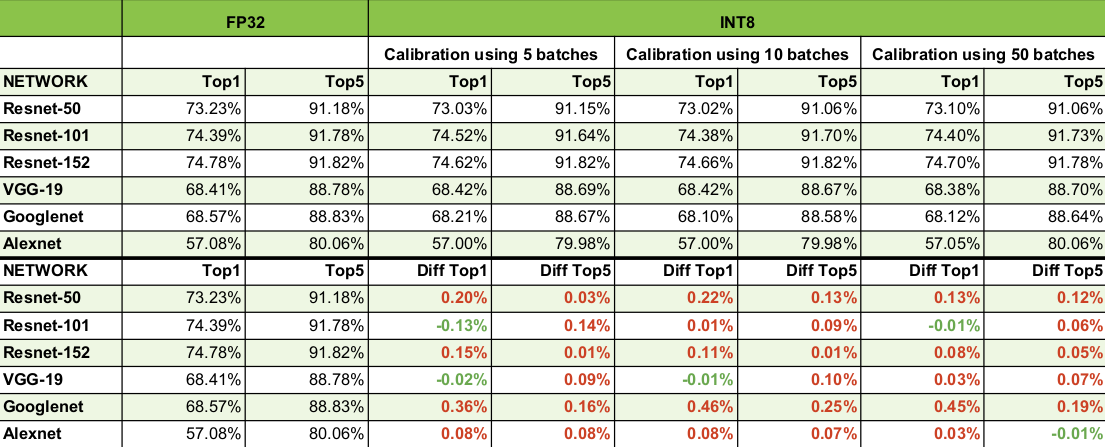
Fig 5.에서 확인할 수 있듯이, 대부분 소수점대의 정확도 감소를 보여준다. 이렇게 좋은 결과가 나온 이유에 대하여 추론해보자면, dropout 등을 통해 이미 딥러닝 네트워크가 몇 가지 parameter들이 제거된 상태에서의 추론도 학습해보았기 때문인 것 같다. 다만 여전히 각 parameter들이 어느정도 영향력을 가지는 지는 분석할 수 없기에, edge case에 대해서 추론이 실패하지 않을 것이라고는 보장할 수 없을 것이다. (개인적으로는 그렇게 크게 문제가 될 것 같아 보이지는 않는다. 따라서 post training quantization은 여전히 작동 가능한 최적화 옵션 중 하나라고 생각한다.) 

 

Fig 6. 기존 네트워크와 TensorRT를 통해 양자화된 네트워크의 추론 속도 비교 [2]

 

Fig 6.은 기존 네트워크 대비 TensorRT를 통해 양자화된 네트워크의 추론 속도 향상을 보여주는 표이다. 모든 경우에서 추론 속도 향상이 있으며, batch size가 커질수록 2X, 3X 이상의 추론 속도 향상을 보여준다. Calibration을 통해 정확도 하락이 크지 않으면서도 어느정도 speed-up을 달성하는 것을 보면, PTQ(TensorRT)는 충분히 제품 레벨에서 사용할 만한 옵션이 될 것 같다.

 

 

 

Reference

[1] https://docs.nvidia.com/deeplearning/tensorrt/developer-guide/index.html#working-with-int8

[2] Szymon Migacz, 8-bit Inference with TensorRT, NVIDIA May 8, 2017

[3] https://en.wikipedia.org/wiki/Kullback%E2%80%93Leibler_divergence