| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- Qubit
- deep_learning
- cloud
- 쿠버네티스
- convolution
- C++
- jhDNN
- GPU
- CuDNN
- dnn
- quantum_computing
- CUDA
- 양자역학의공준
- Compression
- 딥러닝
- nvidia
- SpMM
- flash_memory
- 반도체
- stl
- Semiconductor
- DRAM
- 클라우드
- FPGA
- 반도체기초
- sycl
- kubernetes
- HA
- POD
- jhVM
- Today
- Total
Computing
Distributed Deep Learning Training (분산 딥러닝 개념, Distributed SGD, Data Parallelism) 본문
Distributed Deep Learning Training (분산 딥러닝 개념, Distributed SGD, Data Parallelism)
jhson989 2022. 7. 26. 22:42딥러닝 학습 과정과 Stochastic Gradient Descent (SGD)
Stochasic Gradient Descent(SGD)는 한국어로 확률적 경사 하강법이라고 하는데, 딥러닝 네트워크를 학습하는 가장 기본적이고 많이 사용되는 방법 중 하나이다. (너무 유명한 개념이라) 간략히 정리하자면, 데이터셋 내 모든 데이터의 gradients를 계산하여 한번에 trainable parameters를 업데이트하는 것이 아닌, 임의로 뽑힌 데이터셋의 subset(= mini-batch)을 이용하여 parameters를 업데이트하겠다는 것이다.

Fig 1.은 하나의 시스템에서 딥러닝 학습 과정을 계산하는 것을 시각적으로 나타낸 그림이다. Database에 input 데이터가 있으며, input 데이터셋에서 랜덤하게 B개의 subset(=mini-batch)을 선택한다. 딥러닝 네트워크는 mini-batch에 대하여 Forward(error 계산)&Backward(gradient 계산) 과정과 Update(weight update) 과정을 반복(매 반복당 mini-batch는 새로 선택)하며, parameter를 업데이트한다.

Weight update 과정에서 대부분의 딥러닝 네트워크는 SGD를 활용한다. t시간의 weights를 w_t, (t+1)시간의 weights를 w_(t+1), delta_f를 gradient, B를 mini-batch 사이즈, 알파를 learning rate 라고 할때, SGD 업데이트는 Eq 1.과 같이 표현할 수 있다. Eq 1.에 따르면 B개의 input(데이터)에 대하여 각각의 gradient를 구한 후, 그 값의 평균을 이용해 weight update를 진행한다.
Distributed Deep Learning Training
Fig 1.과 Eq 1.을 보면 알겠지만, Forward 과정에서는 A set of parameters를 이용하여 B개의 데이터 각각의 error를 구한다. 그 후 Backward 과정에서는 구해진 error를 이용하여 gradients를 계산한다. 마지막으로 구해진 gradients의 평균을 이용해 A set of parameters를 업데이트(Update 과정)한다. 이때 B개의 데이터 각각의 error를 구하는 과정과 gradient를 구하는 과정은 동일한 a set of paramters를 읽기만 하기에(read-only 데이터 공유) 쉽게 병렬로 처리가능한다.
반면에 gradient들을 통해 parameters를 업데이트하는 것은 gradient의 평균을 구하고, 공유 데이터에 쓰기를 수행하기에 병렬처리를 쉽게 구현하기 어렵다.
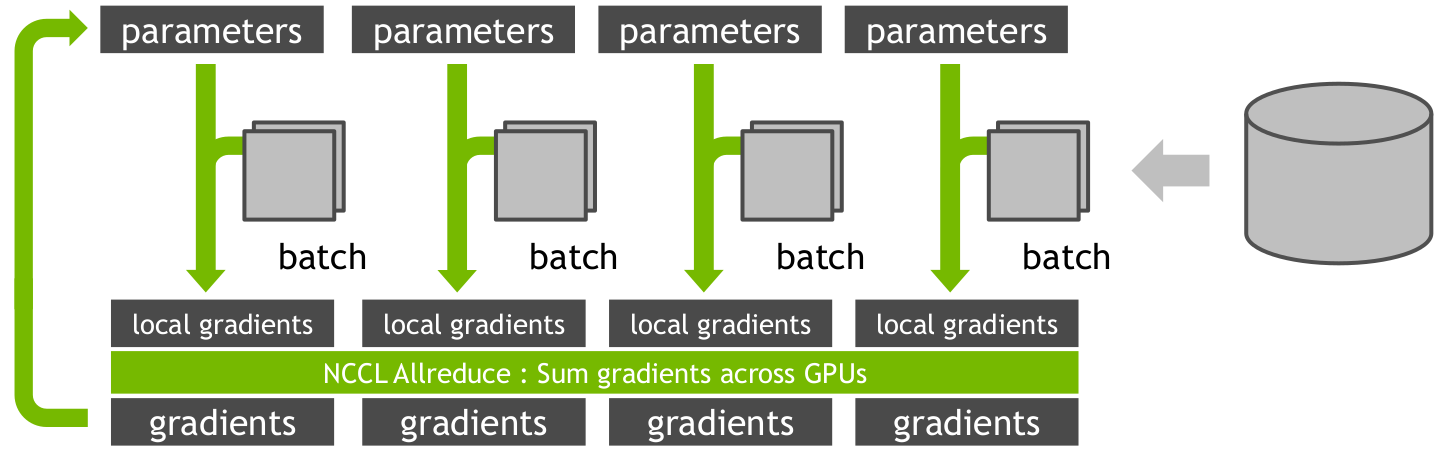
Fig 2.는 4개의 컴퓨터에서 딥러닝 학습을 병렬로 계산하는 것을 그림으로 표현한 것이다. 앞서 설명했듯 B개의 mini-batch를 4등분하여 4개의 컴퓨터가 나눠가진다. parameters의 경우 4개의 컴퓨터에 공유한다. 이 후, 4대의 컴퓨터는 각자만의 4등분 데이터에 대하여 gradients를 구한다. 이때 구분을 위해 이것을 local gradients라고 한다. 이후 4대의 컴퓨터에 나눠져 있는 local gradients들의 모두 모아, B개의 mini-batch에 대한 gradients를 계산한다. 이 gradients의 평균을 구하여 parameters를 업데이트한다.
local gradients를 구하는 것까지는 병렬 계산을 쉽게 설계할 수 있다. 하지만 local gradients를 모은 gradients를 구하고, 공유된 parameters를 업데이트하는 과정은 여러가지 방법으로 구현할 수 있다. 아카데미아에서 구체적으로 분류한 것은 아직 보지 못했는데, 개인적으로 강의자료 [2]를 참고하여 SGD with all-reduce 또는 parameter server model 두 가지로 분류하고자 한다. (2가지 방법 모두 data parallelism을 활용한 것으로, 이것 외에도 model parallelism을 이용한 분산 학습도 존재한다.)
Fig 2.은 SGD with all-reduce 방식을 사용한 것으로, update 과정 또한 병렬로 처리가 된다. Parameter server model은 구현에 따라서 병렬로 구현할 수도 있지만, 기본적인 원리는 순차 처리를 바탕으로 한다.
SGD with all-reduce

앞서 말했듯, Fig 2.은 SGD with all-reduce 방식을 사용한 distributed 딥러닝 학습이다. Fig 2.은 1대의 database와 4대의 컴퓨터로 구성된 분산(distributed) 시스템으로, 4대의 컴퓨터가 함께 딥러닝 학습을 진행한다. 1대의 database에는 학습 데이터가 위치한다.
SGD with all-reduce는 다음과 같이 작동한다.
1. 4대의 컴퓨터는 모두 동일한 parameters 복사본을 가짐
2. 각 컴퓨터는 database에서 랜덤한 데이터(local mini-batch)를 선택
3. 각 컴퓨터는 랜덤 선택된 데이터에 대하여 Forward & Backward 과정을 거쳐, 각자만의 local gradients를 계산
- 각 컴퓨터의 입력 데이터가 다르기에, 각 컴퓨터의 local gradients는 각기 다른 값을 가짐
4. All-reduce 연산을 통해 local gradients들을 합친 gradients를 계산하고, 그것을 모든 컴퓨터에 다시 전달
- All-reduce 연산은 다음을 참고
- local gradients들을 합친다는 것은 여기서는 평균을 구한다는 것
- 모든 컴퓨터에 전달된 gradients는 local gradients들의 평균으로 모두 같은 값임
5. Gradients을 이용하여 parameters를 업데이트
- 모든 컴퓨터에 전달된 gradients와 parameters가 모두 같으니, 업데이트된 parameters 값도 같음
SGD with all-reduce는 학습이 수렴할 때까지 2번부터 5번까지 과정을 반복한다. Parameters와 local mini-batch를 이용해 local gradients를 구하는 과정은, 4개의 mini-batch 각각의 gradients를 순차적으로 구하는 것과 계산 상에 크게 다른 점은 없을 것이다. (다만 batch normalization도 따로 계산하는 지는 확인해 봐야겠다. 아마 그러지 않을까 싶은데)
중요한 것은 parameters의 복사본을 4대의 컴퓨터가 나눠 가지고 있고, 모든 컴퓨터가 나눠가진 이 값들은 학습이 끝날 때까지 서로 같은 값을 유지해야 한다는 것이다. 따라서 All-reduce를 이용한 공통된 gradients 계산 및 broadcast(나눠줌)이 필수이다. All-reduce와 같은 collective communication 패턴은 구현 및 최적화가 매우 어려운 통신 패턴으로, 따라서 SGD with all-reduce는 구현 및 최적화가 어렵다.
Parameter Server Model
SGD with All-reduce 방식은 모든 컴퓨터가 parameters 복사본을 가지고 있도록 한다면, Parameter server model은 하나의 server에 parameter를 저장하는 방식이다.

Fig 3.은 parameter server model을 나타낸 것이다. 그림에서 보듯 parameter server model에는 1대의 parameter server, 1대의 database, M개의 worker 컴퓨터가 참가한다. Parameter server는 네트워크 parameters를 저장하고 있으며, database는 데이터셋을 저장하고 있다.
학습 과정은 다음과 같다.
1. M개의 worker들은 parameter server에서 parameters를, database에서 local mini-batch를 전달받음
- parameters는 공통된 값이지만, local mini-batch는 worker마다 다름
2. 이것들을 통해 모든 worker 컴퓨터들은 forward & backward 과정을 거쳐 local gradients를 계산함
3. 계산된 local gradients를 parameter server에 전송
4. Parameter server는 모든 local gradients들을 평균내에 gradients를 계산하고, parameters를 업데이트
Parameter server model은 학습이 수렴할 때까지 2번부터 5번까지 과정을 반복한다. 학습과정에서 보듯, 해당 모델의 경우 parameter 값을 parameter server가 유일하게 가지고 있고, worker들은 그 값을 복사 받아와서 계산하는데만 사용한다. 따라서 worker가 아무리 늘어나더라도 쉽게 구현이 가능하다. Parameter를 복사해주고, local gradients만 받아오면 되기 때문이다. (Scailablity가 매우 좋다.)
하지만 parameter 저장만을 위한 추가적인 한대의 컴퓨터가 더 필요하고, M개의 workers가 1개의 parameter server에 local gradients를 전송하는 과정은 병렬화가 불가능하기에 성능 향상에 한계가 있다. (1번 worker가 server로 보내고, 그 다음 1번 worker가 server로 보내고, 그 다음 ...., 마지막으로 M번 worker가 server로 보내고) 사실 All-reduce같은 경우 OpenMPI, NCCL과 같은 최적화된 집합 통신(collective communication) 라이브러리를 사용하면 되기에, parameter server model보다 SGD with All-reduce model이 성능이 더 좋을 수 있다. (물론 네트워크 환경 및 컴퓨터 개수, 어떤 네트워크 인지 등등에 따라 달라지겠지만..)
Reference
[1] Sylvain Jeaugey, DISTRIBUTED DEEP NEURAL NETWORK TRAINING: NCCL ON SUMMIT, NVIDIA
[2] Christopher De Sa, Distributed Machine Learning and the Parameter Server, lecture note on Principles of Large-Scale Machine Learning(Spring 2020), cornell
[3] J. Chen, R. Monga, S. Bengio, and R. Jozefowicz. Revisiting distributed synchronous sgd. In International Conference on Learning Representations Workshop Track, 2016.
[4] https://en.wikipedia.org/wiki/Stochastic_gradient_descent
'Deep Learning > Optimization (Algorithm)' 카테고리의 다른 글
| TensorRT (3) TF-TRT (TensorFlow integaration with TensorRT) 소개 및 구현 예제 (0) | 2022.07.18 |
|---|---|
| TensorRT (2) 설치 및 샘플 테스트 (Ubuntu 18.04 기준) (0) | 2022.07.08 |
| Compression - 4 : Quantization (2) Post Training Quantization 분석 (Calibration, TensorRT) (0) | 2022.06.16 |
| Compression - 3 : Quantization (1) 기본 아이디어 및 핵심 (0) | 2022.06.15 |
| TensorRT (1) 개념, 최적화 방법, Workflow (Layer Fusion, Quantization 등) (0) | 2022.06.14 |



