| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
- DRAM
- jhDNN
- HA
- Semiconductor
- sycl
- CUDA
- dnn
- Compression
- SpMM
- quantum_computing
- cloud
- stl
- FPGA
- POD
- CuDNN
- deep_learning
- flash_memory
- 양자역학의공준
- 쿠버네티스
- 반도체
- 반도체기초
- kubernetes
- Qubit
- jhVM
- convolution
- 딥러닝
- GPU
- nvidia
- C++
- 클라우드
- Today
- Total
Computing
양자 알고리즘 (1) : Deutsch's Algorithm 도이치 알고리즘 본문
양자 알고리즘 (1) : Deutsch's Algorithm 도이치 알고리즘
jhson989 2022. 5. 17. 21:11이 자료는 김태현 교수님의 양자 컴퓨팅 및 정보의 기초 강의를 바탕으로 정리하였습니다.
양자 알고리즘의 필요성 : 관측의 저주
양자 컴퓨팅의 장점은 양자의 superposition (중첩) 성질을 활용한 양자 병렬성을 이용할 수 있다는 것이다. 기존의 디지털 회로의 한 bit는 0과 1 중에 하나의 상태만을 가질 수 있다. 예를 들어 1bit를 나타내는 하나의 cell 내 전압이 5V 이상이면 신호 1로 해석하고, 0V에 가까우면 신호 0으로 해석한다. 그에 비해 양자 회로의 한 qubit는 양자의 superposition 성질을 이용하여 0 또는 1 뿐만 아니라 0과 1 상태를 동시에 가질 수 있다. 이전 포스터에서 볼 수 있듯, 이러한 중첩 상태의 qubit를 이용하면 qubit가 0일 때의 값과 1일 때의 값을 한번에 병렬 계산할 수 있다. 만약 n개의 qubits로 수를 표현한다면 2^n 만큼의 수를 중첩하여 저장할 수 있으며, 이를 통해 2^n 번의 계산을 병렬로 처리할 수 있다.
이전 포스터에서 언급했듯이 양자 병렬성을 곧바로 도입하기에는 한계가 존재한다. 바로 관측 시 양자들의 superposition 상태가 붕괴되어 하나의 상태로 고정된다는 것이다. 다음과 같은 문제 상황이 있다고 하자.
어떤 함수 F(x) : {0,1} -> {0,1} 에 대하여, F(0)과 F(1)이 같은 지를 판단해라
일반적인 디지털 논리회로에서는 F(0)과 F(1) 각각 하나씩 직접 계산해서 값을 구한 이후, 그 둘의 값을 비교할 것이다. 이 경우 F(x) 계산을 두 번 하여야 한다. 하지만 양자회로에서는 x가 0과 1 상태 모두를 가질 수 있기에, 한번의 계산으로 F(0)과 F(1)을 구할 수 있지 않을까 생각할 수 있다. 하지만 Fig 1.과 같은 한계를 가진다.
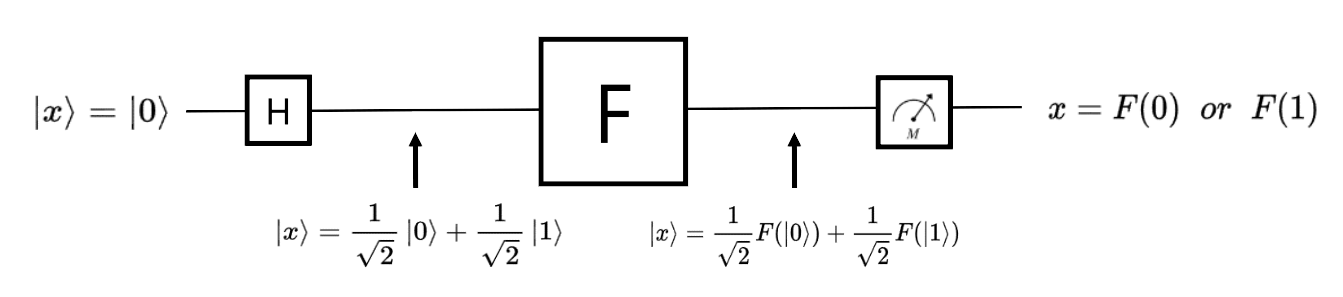
Fig 1. 처럼 |x⟩를 |0⟩으로 초기화한 후 hadamard gate를 통과하면 |x⟩는 |0⟩, |1⟩의 중첩 상태가 된다. 중첩된 |x⟩를 함수 F를 나타내는 양자회로를 통과시키면 |x⟩는 F(|0⟩), F(|1⟩)의 중첩 상태가 된다. 따라서 한번의 계산으로 F(|0⟩), F(|1⟩)의 값을 계산해 내었다. 문제는 양자의 결과를 관측하고자 할 때 발생한다. 중첩된 양자는 코펜하겐의 해석에 따라 관측 시 하나의 상태로 붕괴한다. 즉 관측 전의 |x⟩는 F(|0⟩), F(|1⟩)의 정보를 모두 가지고 있지만, 그 값을 알기 위해 관측하게 될 경우 x의 값은 F(|0⟩), F(|1⟩) 둘 중 하나로 결정된다. 따라서 양자 회로를 사용하더라도 디지털 회로와 마찬가지로 2번 이상 F(x)의 값을 계산해야 한다.
따라서 양자 병렬성을 활용하려면 관측하기 전에 값을 알 수 있는 새로운 알고리즘이 필요하다. 이러한 양자 컴퓨터 상에서 양자 병렬성을 활용할 수 있도록 하는 알고리즘을 양자 알고리즘이라고 하며, 이를 통해 기존의 컴퓨터가 오랜 시간 걸려 풀던 문제를 극한의 병렬처리를 통해 풀고자 한다.
Deutsch's Algorithm
데이비드 엘리에저 도이치(David Elieser Deutsch)는 옥스퍼드 대학교 교수로, 위 문제를 한번의 계산할 수 있는 Deutsch's algorithm[1]을 제안하였다. 도이치 알고리즘의 핵심은 양자의 superposition과 양자들 간의 interference (or entanglement)를 활용하도록 하는 것이다.
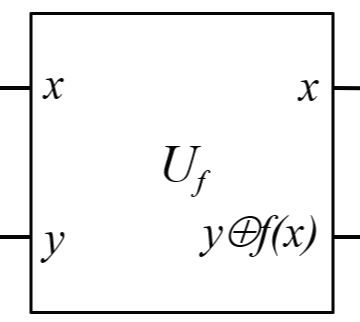
Fig 2. 는 도이치 알고리즘에 사용되는 양자 회로를 나타낸 블록이다. 위 블록은 |x,y⟩가 입력으로 들어오면 |x,y⊕F(x)⟩를 출력한다. 이때 ⊕ 연산은 두 값을 더한 후 2로 나눈 나머지를 구하는 연산이다.
우리는 Eq 1. 과 같이 Uf의 결과를 일반화 할 수 있다.
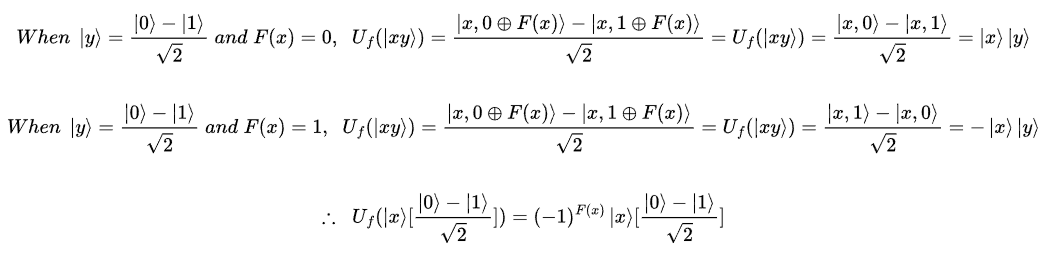
Uf를 이용하여 다음 Eq 2. 와 같이 정리할 수 있다.
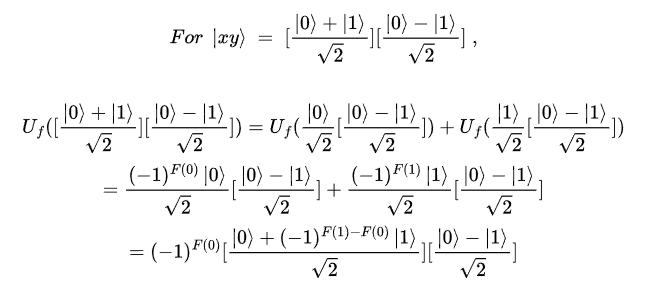
만약 F(0) = F(1)이라면

F(0) != F(1)이라면

이 될 것이다. (앞의 부호는 생략되었는데, 부호는 측정 시 무시되기에 계산 자체에서 빼도 된다. 이러한 부호를 global phase라고 한다.)
따라서 정리하자면 다음과 같은 회로가 있으면 우리는 F(0)와 F(1)이 같은 지 다른 지를 한번의 계산만으로 알 수 있다.
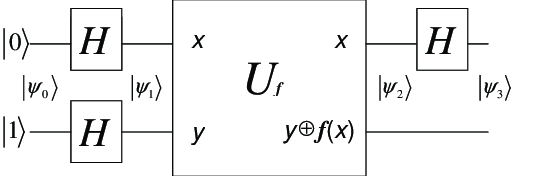
만약 F(0) = F(1) 이라면 Uf를 통과한 |x⟩ = (|0⟩+|1⟩)/sqrt(2)가 될 것이고, 이것을 마지막 hadamard gate를 통과시키면 |x⟩ = |0⟩이 될것이다. 반대로 F(0) != F(1) 이라면 Uf를 통과한 |x⟩ = (|0⟩-|1⟩)/sqrt(2)가 될 것이고, 이것을 마지막 hadamard gate를 통과시키면 |x⟩ = |1⟩이 될것이다. 따라서 우리는 마지막 |x⟩ 값이 |0⟩인지 |1⟩인지를 측정한다면 한번의 F(x) 연산만으로 F(0)과 F(1)이 같은 지 아닌 지를 판단할 수 있다.
Reference
[1] Deutsch, David (July 1985). “Quantum theory, the Church-Turing principle and the universal quantum computer” (PDF). 《Proceedings of the Royal Society of London; Series A, Mathematical and Physical Sciences》 400 (1818): pp. 97–117. Bibcode:1985RSPSA.400...97D. doi:10.1098/rspa.1985.0070
[2] https://en.wikipedia.org/wiki/Quantum_algorithm#Deutsch%E2%80%93Jozsa_algorithm
[3] Demonstration of Deutsch's Algorithm on a Stable Linear-Optical Quantum
Computer - Scientific Figure on ResearchGate. Available from: https://www.researchgate.net/figure/Quantum-circuit-of-Deutschs-algorithm-H-is-the-Hadamard-gate_fig2_46585390 [accessed 17 May, 2022]
'가속기 Accelerator > Quantum Computing' 카테고리의 다른 글
| 양자컴퓨팅 - 5 : 양자 병렬성 및 양자 회로 특징 (Toffoli gate) (0) | 2022.05.06 |
|---|---|
| 양자컴퓨팅 - 4 : Quantum Entanglement (양자 얽힘, 슈뢰딩거의 고양이) (0) | 2022.05.02 |
| 양자컴퓨팅 - 3 : Quantum Circuit & No Cloning Theorem (0) | 2022.04.25 |
| 양자컴퓨팅 - 2 : Two Qubits Gate & Tensor Product (0) | 2022.04.06 |
| 양자컴퓨팅 - 1 : Qubit & Gate (0) | 2022.03.28 |




