양자컴퓨팅 - 2 : Two Qubits Gate & Tensor Product

2022.03.28 - [가속기 Accelerator/Quantum Computing] - 양자컴퓨팅 - 1 : Qubit & Gate

이 자료는 김태현 교수님의 양자 컴퓨팅 및 정보의 기초 강의를 바탕으로 정리하였습니다.

Two Qubits Gate

양자컴퓨팅 : Qubit & Gate

앞서 qubit과 single qubit을 입력으로 받는 gate들에 대하여 정리하였다. 오늘 qubit 입력을 두개를 받는 two qubits gate에 대하여 정리하고자 한다.

 

양자 회로는 모든 디지털 논리 회로를 표현할 수 있다고 한다. 그것을 위하여 AND gate, OR gate와 같은 two bits를 입력으로 받는 gate 또한 양자 게이트로 표현할 수 있어야 한다. 따라서 단순히 single qubit을 조작하는 pauli X, Y, Z gate 뿐만 아니라 2 qubits을 입력으로 받는 gate가 필요하다.

 

지금까지 배웠던 양자 표현법은 하나의 양자만을 표현할 수 있었다. 양자 A, B가 있을 때, Fig 1과 같이 A, B를 독립적으로 표현할 수 있다.

Fig 1. Single quantum 표현법

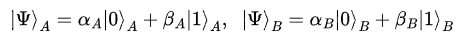
하지만 Two qubits gate의 경우 두개의 양자의 상태를 한번에 표현할 필요가 있다. 2개 양자의 경우, Fig 2.와 같이 총 4개의 상태가 있을 수 있다.

Fig 2. Two qubits의 가능한 상태

두 vector spaces의 tensor product는 두 vector spaces가 결합된 하나의 새로운 vector space를 정의할 수 있다. 

 

 

 

Tensor Product

두 hilbert vector spaeces V, W에 대하여 tensor product V⊗W는 새로운 hilbert vector space를 정의하고, 이때 새로운 vector space는 Eq 1.을 만족한다. 

Eq 1.

V의 orthonormal basis를 |i⟩, W의 orthonormal basis를 |j⟩라고 할 때, V⊗W의 basis는 |i⟩⊗|j⟩이다. V⊗W 공간에 속한 vector는 linear combination of |x⟩⊗|y⟩, where |x⟩∈V and |y⟩∈W, 로 표현되며 편의를 위해  |xy⟩ (ex, |00⟩, |01⟩, |10⟩, |11⟩)로 표현할 수 있다.

 

V space 상에 정의된 linear operator A, W space 상에 정의된 linear operator B에 대하여, A⊗B on V⊗W는 Eq 2.와 같이 정의한다. Operator A⊗B on V⊗W는 linearity를 가진다.

Eq 2. A ⊗B on V ⊗W의 정의

 

Tensor product는 Kronecker product와 같이 행렬 표현이 가능하다. A가 m*n matrix, B가 p*q matrix라고 할 때 Fig 3.과 같은 형태를 가진다.

Fig 3. Tensor product of A and B 행렬 표현법 [3]

 

 

 

Controlled-Not Gate

Controlled-Not gate는 2개의 qubits을 입력으로 받는 binary operator이다. 디지털 논리 회로에서 XOR와 같은 진리표를 가진다.

Fig 4. Controlled-Not gate의 표기법과 진리표 [2]

사실 디지털 논리 회로에서 binary operator는 두 개의 입력을 받으면 하나의 출력을 낸다. 만약 a xor b = 1이라고 할 때 우리는 a, b의 정확한 값을 알 수 없다. a=1,b=0 이거나 a=0,b=1일 수 있다.

 

하지만 양자 회로에서는 binary operator에 의해 한 qubit의 상태가 조작될 뿐 두 개의 qubits의 정보는 여전히 보존된다. 따라서 Fig 4.와 같이 x CNOT y을 계산하더라도 x의 정보는 사라지지 않고 유지되며, 그에 따라 출력만 알면 CNOT 게이트의 입력이 무엇인지 알 수 있다. 디지털 논리 회로에서도 Fig 4.와 같이 x의 값을 유지해주면 되지 않냐라고 할 수 있지만 디지털 논리 회로에서는 새로운 wire를 추가해줘야 데이터가 유지되는 것이다. Gate 하나만을 놓고 생각하면 정보의 손실(입력 2 bits -> 출력 1 bit)은 무조건 발생한다. 그에 비해 양자 회로에서 CNOT gate는 정보의 손실이 없으며(입력 2 qubits -> 출력 2 qubits), 그것은 gate가 입력의 한 양자의 상태만을 조작하기 때문이다. (이 덕분에 엄청난 에너지 효율을 달성할 수 있다고 한다.)

 

x ∈ X, y ∈ Y에 대하여, CNOT gate는 Fig 5.와 같은 행렬 표현이 가능하다.

Fig 5. CNOT gate의 행렬 표현법

 

 

Reference

[1] https://en.wikipedia.org/wiki/Kronecker_product

[2] https://en.wikipedia.org/wiki/Controlled_NOT_gate