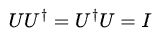| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| 8 | 9 | 10 | 11 | 12 | 13 | 14 |
| 15 | 16 | 17 | 18 | 19 | 20 | 21 |
| 22 | 23 | 24 | 25 | 26 | 27 | 28 |
| 29 | 30 | 31 |
- nvidia
- flash_memory
- cloud
- GPU
- jhDNN
- convolution
- stl
- SpMM
- Compression
- deep_learning
- POD
- FPGA
- 클라우드
- 양자역학의공준
- DRAM
- dnn
- quantum_computing
- CUDA
- Qubit
- sycl
- Semiconductor
- 딥러닝
- CuDNN
- 반도체
- jhVM
- kubernetes
- 반도체기초
- 쿠버네티스
- HA
- C++
- Today
- Total
Computing
양자역학의 공준 2 : 입자 상태의 진화 본문
이 자료는 김태현 교수님의 양자 컴퓨팅 및 정보의 기초 강의를 바탕으로 정리하였습니다.
Postulate 2
The evolution of a "closed" quantum system is described by a unitary transform
시간에 따른 닫힌 양자의 상태 변화는 unitary transform matrix로 표현 가능하다. (Unitary matrix에 대한 설명은 밑에 추가하였다.)
X가 unitary matrix일 경우, 양자의 다음 상태는 다음 식으로 계산할 수 있다.

예를 들어 2개의 ket |0⟩, |1⟩ 를 기저로 하는 벡터 공간에서 , 다음과 같은 unitary matrix X, unitary matrix H에 의해서 양자 상태가 진화한다고 하자.

그렇다면 이때 2개의 ket |0⟩, |1⟩의 X, H에 의해 변환된 다음 상태는 그림과 같이 계산 가능하다.
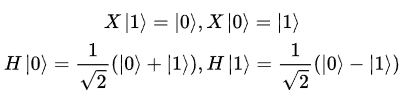
Adjoint of an matrix
Unitary matrix 설명에 앞서 adjoint라는 개념을 알아야 한다.
복소 벡터공간에서 matrix의 adjoint는 실수 벡터공간에서의 matrix의 transpose의 개념과 같다.

즉 전치행렬 + complex conjugate를 하면 된다. (저 십자가는 dagger라고 발음한다.)
Ket |V⟩의 대응되는 bra는 ⟨V|이다.
그렇다면 ket Ω|V⟩ = |ΩV⟩의 대응되는 bra는 ⟨ΩV|인데, Ω의 adjoint matrix에 대해서는 다음과 같은 성질이 있다.
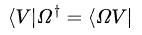
Unitary operation
Adjoint 개념을 알았으면 unitary operation의 개념을 정의할 수 있다.
Definition: an operator U is unitary if
Field를 실수에 한정한다면, orthogonal operation와 같은 개념이다.
'가속기 Accelerator > Quantum Computing' 카테고리의 다른 글
| 양자컴퓨팅 - 3 : Quantum Circuit & No Cloning Theorem (0) | 2022.04.25 |
|---|---|
| 양자컴퓨팅 - 2 : Two Qubits Gate & Tensor Product (0) | 2022.04.06 |
| 양자컴퓨팅 - 1 : Qubit & Gate (0) | 2022.03.28 |
| 양자역학의 공준 3 : 코펜하겐 해석 (0) | 2022.03.17 |
| 양자역학의 공준 1 : 입자의 상태 (0) | 2022.03.09 |